
中学生になったときに、まず壁になるのが「連立方程式」です。
グラフで説明されてもわからないし、ましてや式だけで解き方を覚えても結局何をしていたのかさっぱり覚えていないということはないですか?
ここでは学校で習うのとは違う方法で「連立方程式」を解説していきます。
連立方程式ってなんなの?
まずは問題を考えてみよう
連立方程式とは何のかを説明していく前に問題を出します。
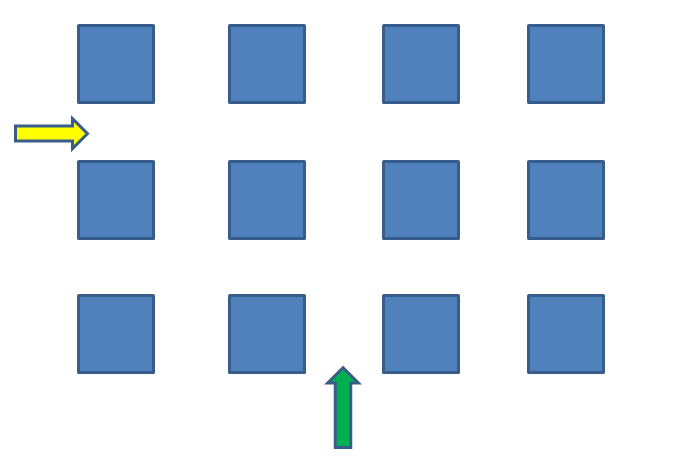
図のように、黄色と緑の矢印の位置から、そのまま矢印の示す方向へ真っ直ぐ進む人物がそれぞれ1人いるとします。
どこで出会いますか?
答えはすぐに分かりますよね。
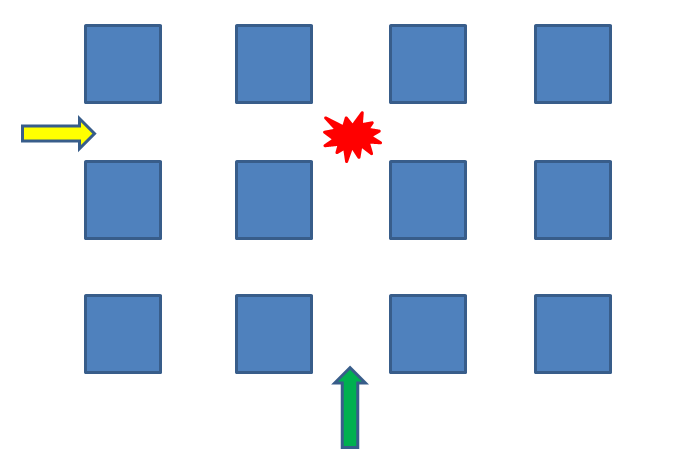
赤い印の地点で出会うはずです。(通り過ぎて出会わないとかは無しとします。)
はい!連立方程式が解けました。
そうです。これが連立方程式です。簡単でしょ?
連立方程式ってどういうときに使えるの?
連立方程式とは、進行方向がわかっている2つのものが出会う場所を知りたいときに使用します。
先ほどの問題では、2人とも真っ直ぐに進むことがわかっていました。

進行方向を図で表すと、直線になりますよね。
一番初めに習う連立方程式は、直線を考えたと思います。それが一番簡単だからです。
ここで重要なのは、「進行方向がわかっている」ということです。つまり、どう動くのかさえ把握できるのであれば、直線でなくてもいいのです。

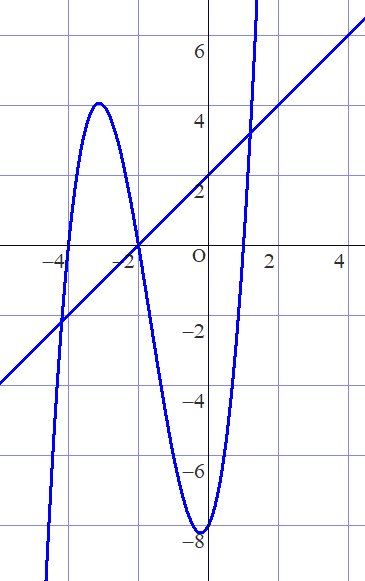
このように少々めんどくさそうなものも、進む方向さえわかっているのであれば、どこで出会うのかがわかるというのが連立方程式です。
つまり、交点を求めるときに連立方程式を使用します。
連立方程式で解けない問題って?
連立方程式は、2つのものが出会うところを求めました。
では、「出会わないときってどうなの?」って疑問が当然出てくるでしょう。
2人がどれだけ進んでも出会わないときってどういうときか考えてみましょう。

そうです。同じ方向へ進んでいるときですよね。
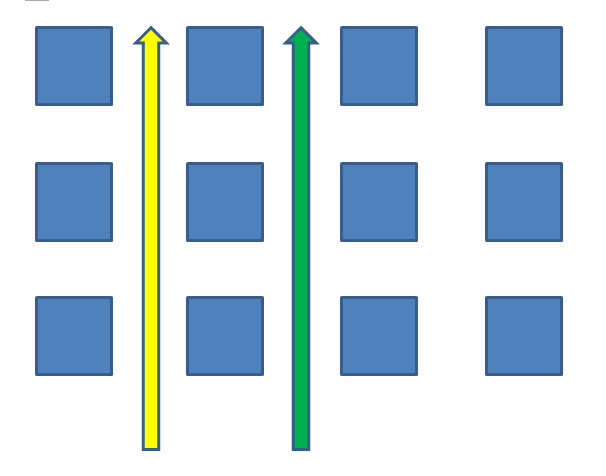
2人の関係が平行な場合は、連立方程式で答えが出ることはありません。
連立方程式は、あくまでも出会う場所を知ることができるだけなので、出会わないことがわかっているならばそれは解けないのです。
まとめ
- 連立方程式は、2人の出会う場所を把握します。
- 連立方程式は、2人が出会わなければ解けません。
これをもう少し授業寄りに書き直すとこうなります。
- 連立方程式は、グラフの交点を求めます。
- 連立方程式は、グラフが平行な場合、解けません。
あとがき
難しい問題になると、範囲を場合分けしたりするので、平行でなくても解けない(解けても答えではない)場合が出てくるのですが、今は知らなくても大丈夫です。そのうち分かるようになります。
とりあえず、これだけ把握しておけば、高校卒業までは問題なしです。
応用問題になりますが、直線が3本あっても同様です。交点を求めるのであれば連立方程式。連立方程式を解けば交点が自動的に出てきます。
3次元になっても、平面になっても同様です。計算はめんどくさいですが、考え方は覚えておきましょう。

コメント